Opis & Analiza gry "Mała ewolucja"
Mała Ewolucja - Wprowadzenie

Matematyczna teoria gier zastosowana do procesów ewolucyjnych pozwoliła znaleźć odpowiedź na pytanie: "Dlaczego stosunek liczby drapieżników do liczby ich ofiar pozostaje w danej populacji mniej więcej stały?". Badacze analizujący prosty model takiej populacji doszli do wniosku, że to jak sobie dany gatunek radzi sobie w realizacji celu życia zależy od liczby drapieżników i ich ofiar w populacji.
Gdy w populacji dominują drapieżniki, paradoksalnie zwiększa to szanse ofiar na przeżycie i rozmnożenie - drapieżniki bowiem mają mniejsze szanse na ich upolowanie, rośnie również konkurencja pomiędzy nimi. Natomiast gdy jest więcej ofiar to wzrastają szanse drapieżników - mają więcej pokarmu, łatwiej go upolować i nikt nie przeszkadza w ich zjedzeniu. Dzięki temu w kolejnych pokoleniach stosunek liczby drapieżników do ich ofiar pozostaje względnie stały.
Najważniejszy wniosek jaki płynie z analizy gier ewolucyjnych jest taki, że szanse danego osobnika na realizację celu życia zależą właśnie od stosunku liczby drapieżników do liczby ich ofiar w danej populacji.
Mała Ewolucja - Opis Zasad Gry

Klasyczna dla Fizyki Życia gra ewolucyjno-społeczna – model społeczeństwa złożonego z osobników – obiektów samodzielnych, czerpiących z zasobów.
Gra nałożona na populację złożoną z N osobników. Co pewien czas odbywa się runda, podczas której wszyscy ci osobnicy są losowo dobierani w pary i rozgrywają pomiędzy sobą tak zwaną grę pojedynczego spotkania. W zależności od stosowanej przez osobnika (gracza) strategii każdy z nich zdobywa lub traci punkty. To ile tych punktów zdobywa lub traci określa funkcja wypłat, której argumentami są strategie osobników biorących udział w grze pojedynczego spotkania. Punkty te są sumowane na indywidualnym koncie każdego z osobników, po czym rozpoczyna się następna runda.
Kluczowe w tej grze są przepisy o selekcji, klonowaniu i odtworzeniu populacji. Polegają one na tym, że co pewien czas, na przykład po „zaledwie” trzech lub „aż” po milionie takich rund, cała grupa (populacja) uczestników zostaje poddana działaniu funkcji selekcyjnej, która do dalszych rozgrywek przepuszcza, na przykład, 50% osobników – wyłącznie tych, którzy zgromadzili najwięcej punktów. Pozostała część zostaje odrzucona i już dalej nie bierze udziału w grze – można powiedzieć, że zostaje unicestwiona. Ci natomiast, którzy selekcję przechodzą, są klonowani, konta wszystkich są zerowane, i rozgrywka zaczyna się od początku. Jak nietrudno zauważyć, po operacji selekcji i reprodukcji liczebność populacji pozostaje na poziomie wyjściowym.
Doprecyzujmy pojęcia:
-
Liczebność Populacji
 - głównym założeniem tej gry jest stałość liczebności populacji. W naszym przypadku liczebność ta wynosi N.
- głównym założeniem tej gry jest stałość liczebności populacji. W naszym przypadku liczebność ta wynosi N.
-
Skład Populacji
 - cała populacja składa się z dwóch rodzajów osobników: Złodziei i Producentów. Nazwy te są umowne, określają jednak charakter zawodnika. I tak Złodzieje nic nie dają, natomiast Producenci wypracowują punkty. Pojęcie "skład populacji" określa procentowy udział Producentów i Złodziei w populacji.
- cała populacja składa się z dwóch rodzajów osobników: Złodziei i Producentów. Nazwy te są umowne, określają jednak charakter zawodnika. I tak Złodzieje nic nie dają, natomiast Producenci wypracowują punkty. Pojęcie "skład populacji" określa procentowy udział Producentów i Złodziei w populacji.
-
Gra Pojedynczego Spotkania
 - gra odbywana w parze dwóch losowo dobranych osobników, w wyniku której obaj otrzymują lub tracą punkty. O tym kto i ile ich otrzymuje decyduje Macierz Wypłat. Zapisane są w niej informacje, że jeśli na przykład spotka się Złodziej ze Złodziejem to obaj tracą po 25 punktów.
- gra odbywana w parze dwóch losowo dobranych osobników, w wyniku której obaj otrzymują lub tracą punkty. O tym kto i ile ich otrzymuje decyduje Macierz Wypłat. Zapisane są w niej informacje, że jeśli na przykład spotka się Złodziej ze Złodziejem to obaj tracą po 25 punktów.
-
Punkty
 - w grach ewolucyjnych punkty te nazywane są: "survival points" (punkty przetrwania) albo "sharable resources" (zasoby do podziału). Od razu powstaje kilka prostych pytań:
- w grach ewolucyjnych punkty te nazywane są: "survival points" (punkty przetrwania) albo "sharable resources" (zasoby do podziału). Od razu powstaje kilka prostych pytań:
- Skąd się biorą te punkty?
- Dlaczego w wyniku spotkania dwóch osobników i rozegrania pomiędzy nimi gry pojedynczego spotkania mogą oni sięgnąć do zewnętrznej składnicy punktów, wziąć z niej kilkadziesiąt i w jakiś tam sposób rozdzielić je między siebie?
Odpowiedzieć na nie można wyobrażając sobie, że mała ewolucja rozgrywana jest na polanie (źródło trawy, która jest życiowym zasobem [resergią] dla zajęcy) pomiędzy zającami i lisami. Dla lisów zając stanowi życiowy zasób. Z kolei dla trawy życiowymi zasobami są: odchody zajęcy i lisów oraz... energia słoneczna - Słońce jest bowiem tą ostateczną i pierwotną składnicą punktów przetrwania.Podczas spotkania dwóch lisów dochodzi do bezpowrotnej utraty punktów - żaden z nich niczego nie zyskuje, a oba tracą swój czas. Gdy lis spotka się z zającem i jeśli uda mu się go złapać i zjeść to lis przejmuje wszystkie zasoby przetrwania zająca. Gdy dochodzi do spotkania dwóch zajęcy to... mogą się one rozmnożyć powielając siebie jako zasób.
Ogólnie rzecz biorąc punkty z macierzy wypłat w grach ewolucyjnych są resergią - zasobem potrzebnym do przetrwania i rozmnożenia, czyli zasobem potrzebnym do realizacji celu życia.
-
Runda
 - jest to losowy dobór wszystkich osobników w pary, rozegranie między nimi gier pojedynczego spotkania i dodanie ugranych przez nich punktów do ich indywidualnych kont;
- jest to losowy dobór wszystkich osobników w pary, rozegranie między nimi gier pojedynczego spotkania i dodanie ugranych przez nich punktów do ich indywidualnych kont;
-
Selekcja
 - proces selekcji wybiera określony procent osobników np. 50%, którzy zgromadzili największą liczbę punktów. Pozostali są unicestwiani. Populacja po selekcji podlega procesowi Odtworzenia Populacji.
- proces selekcji wybiera określony procent osobników np. 50%, którzy zgromadzili największą liczbę punktów. Pozostali są unicestwiani. Populacja po selekcji podlega procesowi Odtworzenia Populacji.
-
Klonowanie
 - to proces stworzenia n dokładnych kopii danego osobnika. Na przykład sklonowanie Złodzieja daje w wyniku dwóch Złodziei.
- to proces stworzenia n dokładnych kopii danego osobnika. Na przykład sklonowanie Złodzieja daje w wyniku dwóch Złodziei.
-
Odtworzenie Populacji
 - to proces polegający na sklonowaniu wybranych osobników tak, by zachować stałość liczebności populacji.
- to proces polegający na sklonowaniu wybranych osobników tak, by zachować stałość liczebności populacji.
Jak nietrudno zauważyć najprostszym przypadkiem jest, gdy wyselekcjonowana jest połowa osobników, wówczas każdy z nich jest klonowany - z jednego powstaje dwóch takich samych. Natomiast gdy siła funkcji selekcyjnej jest różna od 50% wówczas proces odtworzenia populacji się komplikuje i wymaga precyzyjnego określenia. Na przykład, gdy funkcja selekcyjna jest silna (np. wyselekcjonowanych z populacji jest 10%) wówczas osobnicy klonowani są po wielokroć, natomiast gdy funkcja selekcyjna jest słaba (np. wyselekcjonowanych z populacji jest 90%) wówczas niektórzy z tych, którym udało się przejść przez sito selekcji i tak nie będą klonowani;
W programie zaimplementowano następujący algorytm odtworzenia populacji. -
Cykl
 - ciąg rund zakończony selekcją i odtworzeniem populacji.
- ciąg rund zakończony selekcją i odtworzeniem populacji.
-
Długość Cyklu
 - liczba rund odbywających się w ramach pojedynczego cyklu.
- liczba rund odbywających się w ramach pojedynczego cyklu.
-
Siła Funkcji Selekcyjnej
 - procent osobników z populacji wybranych do procesu odtworzenia populacji.
- procent osobników z populacji wybranych do procesu odtworzenia populacji.
-
Funkcja Wypłat
 - funkcja, której argumentami są strategie używane przez osobników (graczy) biorących udział w grze pojedynczego spotkania, a wynikiem liczba punktów przyznawana każdemu z nich. W klasycznym przykładzie zaproponowanym przez John"a Maynard"a Smith"a funkcja ta jest reprezentowana przez macierz wypłat.
- funkcja, której argumentami są strategie używane przez osobników (graczy) biorących udział w grze pojedynczego spotkania, a wynikiem liczba punktów przyznawana każdemu z nich. W klasycznym przykładzie zaproponowanym przez John"a Maynard"a Smith"a funkcja ta jest reprezentowana przez macierz wypłat.
-
Macierz Wypłat
 - jest to szczególny przypadek funkcji wypłat. Macierz wypłat określa ile punktów przyznawanych jest konkretnemu osobnikowi w zależności od tego jaką strategię stosował on oraz jego przeciwnik w grze pojedynczego spotkania. Konkretnymi przykładami takich macierzy są: Macierz wypłat „Klasyczny Maynard Smith” oraz Macierz wypłat „Jak to w życiu”
- jest to szczególny przypadek funkcji wypłat. Macierz wypłat określa ile punktów przyznawanych jest konkretnemu osobnikowi w zależności od tego jaką strategię stosował on oraz jego przeciwnik w grze pojedynczego spotkania. Konkretnymi przykładami takich macierzy są: Macierz wypłat „Klasyczny Maynard Smith” oraz Macierz wypłat „Jak to w życiu”
Przykład wg. Maynarda Smitha

Podstawowe założenia:
W klasycznym przykładzie tej gry, zaproponowanym przez John"a Maynard"a Smith"a, rozróżnia się wyłącznie dwa typy strategii: (pracusi i złodziei), a macierz wypłat dla gry pojedynczego spotkania wygląda następująco:
|
|
||
|
|
|
|
| Złodziej | Złodziej traci 25 (-25) Złodziej traci 25 (-25) |
Złodziej zyskuje 50 (+50) Producent nie zyskuje nic (0) |
| Producent | Producent nie zyskuje nic (0) Złodziej zyskuje 50 (+50) |
Producent zyskuje 15 (+15) Producent zyskuje 15 (+15) |
To, co chcemy uzyskać, analizując „Małą ewolucję” z taką właśnie macierzą wypłat, to odpowiedź na pytanie: „Która ze strategii – producenta czy złodzieja – jest lepsza?”. Lepsza, czyli dająca większą szansę na przejście przez sito selekcji i co za tym idzie, na sklonowanie. Pamiętajmy, że przymiotnik „lepsza” wartościuje wyłącznie ze względu na stosowane przez nas reguły gry – lepsi to ci, którzy w narzuconych przez grę warunkach gromadzą więcej punktów. Analizę zacznijmy od przypadku skrajnego, gdy populacja złożona jest z samych producentów i jednego złodzieja. Złodziej gromadzi punkty za każdym razem i już po pierwszym spotkaniu plasuje się na czele listy najbogatszych. Co więcej, niezmiennie na niej pozostaje aż do zadziałania funkcji selekcyjnej. Bycie pierwszym gwarantuje mu oczywiście przejście do następnej tury i sklonowanie jego samego oraz stosowanej przez niego strategii. Od tego momentu w populacji jest dwóch złodziei – on i jego klon, reszta to producentów. Obserwujemy zatem tendencję wzrostową liczby złodziei. Teraz rozważmy populację złożoną z jednego producentów i samych złodziei. Producent nie traci punktów, tracą je natomiast złodzieje, walcząc ze sobą nawzajem. Producent przechodzi selekcję, jest sklonowany i w drugiej turze jest już ich dwóch – obserwujemy zatem tendencję do wzrostu liczby producentów.
Klasyczna analiza matematyczna:
Jeden Złodziej w populacji Producentów powiela się, a w sytuacji odwrotnej powiela się Producent funkcjonujący w środowisku Złodziei. Dla takiej macierzy wypłat musi zatem istnieć jakiś stan równowagi. Można go obliczyć w następujący sposób:
Załóżmy, że x to stosunek liczby złodziei do liczby wszystkich osobników,
czyli sumy liczby złodziei i liczby producentów.
E(Z) – wartość zdobytych przez złodzieja punktów w czasie spotkania z losowym
osobnikiem z populacji
E(P) – wartość zdobytych przez producenta punktów w czasie spotkania z losowym
osobnikiem z populacji
P(Z) – prawdopodobieństwo spotkania złodzieja w czasie spotkania z losowym
osobnikiem z populacji
P(P) – prawdopodobieństwo spotkania producenta w czasie spotkania z losowym
osobnikiem z populacji
P(Z) = x
P(P) = 1 - P(Z) = 1-x
E(Z) = P(Z) * (-25) + P(P) * 50 = -25*x + 50*(1-x) = 50-75x
E(P) = P(Z) * 0 + P(P) * 15 = 15*(1-x) = 15-15*x
E(Z) = E(P) oznacza, że przeciętna liczba punktów zdobytych przez producenta lub złodzieja
będzie równa: 50-75*x=15-15*x
Stąd x=7/12
Przy tak dobranej tabeli wypłat w kolejnych turach liczba złodziei ustabilizuje się na poziomie 7/12 populacji, a producenta odpowiednio na poziomie 5/12. Dążnością tego systemu jest stabilne utrzymywanie się proporcji złodziei do producentów w okolicach wartości 7:5. Jaki wniosek płynie z tej analizy? W życiu, podobnie jak w naszej grze, nie ma jednej absolutnie słusznej drogi postępowania, czy też jedynej zwycięskiej strategii, która gwarantuje sukces w każdych warunkach. O tym, która i w jakim stopniu jest lepsza, decyduje między innymi proporcja osobników stosujących każdą z nich. W zależności bowiem od niej raz lepsza jest strategia złodzieja, a raz producenta, może się też zdarzyć, że obie są równorzędne. To bardzo ważny wniosek, szczególnie dla tych, którzy uważają, że pełne zrozumienie życia nierozerwalnie wiąże się z odkryciem jednej jedynej strategii, która pozwoli permanentnie wygrywać na giełdzie! Zmiana warunków zewnętrznych sprawia, że strategia doskonale sprawdzająca się jeszcze dziś jutro może okazać się absolutnie chybiona!
Ludzie, których myślenie zdominowane jest przez myślenie redukcjonistyczne poprzestają na tej analizie i w pełni zgadzają się z wynikiem mówiącym, że stosunek liczby producentów do złodziei zawsze stabilizuje się na pewnym poziomie.
Jednak bardzo ciekawych spostrzeżeń dostarcza symulacja komputerowa. Okazuje się, że nie jest to wszystko takie proste. Dlatego gorąco zachęcam do prestudiowania rozdziału Mała ewolucja - symulacje komputerowe
Mała ewolucja - Program komputerowy

Program "Small Evolution" służy do symulacji komputerowej gry Mała Ewolucja, której zasady opisane są powyżej.
Niniejszy rozdział zawiera:
-
- Opis ustawień startowych
- Opis okna symulacji
-
- Opis przebiegu symulacji
- Opis liczenia średniej
- Opis algorytmu odtworzenia populacji
Instrukcja obsługi programu:
Ustawienia startowe
Po uruchomieniu programu pojawia się ekran ustawień początkowych:
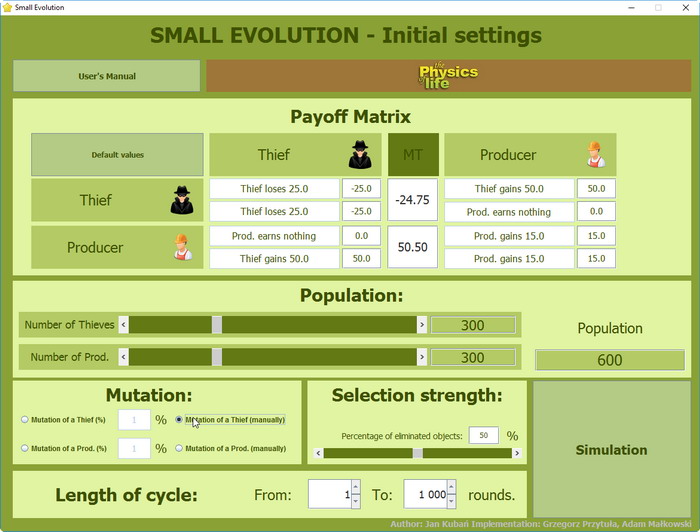
Ekran ustawień początkowych programu do symulacji gry "Mała Ewolucja".
Pierwszym krokiem, który należy wykonać zanim rozpocznie się symulację jest ustawienie wartości początkowych. Ustawić należy następujące grupy parametrów:
-
Macierz wypłat - program uruchamia się z wartościami z poprzedniej sesji. Po naciśnięciu przycisku [Default values] program podstawia wartości zaproponowane przez John"a Maynard"a Smitha. Sekcja ustawień macierzy wypłat {Payoff Matrix} jest wzbogacona o dwie dodatkowe kolumny odpowiedzialne za wprowadzanie mutantów. Na powyższym ekranie widać kolumne z wartościami zmutowanego złodzieja MT (mutated thief) natomiast nie jest widoczna kolumna MP (mutated producer).
-
Liczebność i skład populacji - te parametry wprowadzamy w sekcji {Population}. Przestawiając suwaki wprowadzamy początkową liczbę złodziei i producentów. Liczebność populacji obliczana jest automatycznie i podawana w okienku {Population}.
-
Poziom mutacji. Program umożliwia wprowadzenie do gdy po jednym zmutowanym osobniku. Mutant różni się od swego poprzednika kwotami przyznawanych mu punktów. Wprowadzając odpowiednie wartości można otrzymać na przykład mutanta Złodzieja, który w spotkaniu z innymi Złodziejami otrzymuje nieco więcej punktów natomiast w spotkaniach z Producentami nic się nie zmienia. Program pozwala na dokonywanie mutacji zarówno polepszających jak i pogarszających. Wprowadzanie nowych wartości można dokonywać na zasadzie procentowej lub wprowadzając dane takie jakie się chce.
Decyzję o wprowadzeniu Mutanta podejmujemy klikając w odpowiednie radio buttony w sekcji {Mutation}, a wartości mutantów wprowadzamy w dodatkowych kolumnach macierzy wypłat w sekcji {Payoff Matrix}. -
Siłę selekcji - ten parametr ustawia się w sekcji {Selection strength}. Jeśli ustawimy go na, dajmy na to, 80% oznacza to, że do odtworzenia populacji przeznaczamy wyłącznie 20% osobników, które zgromadziły najwięcej punktów podczas wszystkich rund cyklu.
-
Długość cyklu - ten parametr ustawia się w sekcji {Length of cycle}. Dla każdego cyklu liczbę rund program określa w sposób losowy. W sekcji {Length of cycle} można określić zakres spośród jakiego losowana jest ta liczba. W tym przypadku rund nie będzie mniej niż jedna i nie więcej niż tysiąc.
-
Po ustawieniu wszystkich parametrów startowych można przejść do okna symulacji klikając w przycisk {Simulation}
Okno symulacji
Ekran symulacji służy do pokazywania zmian w badanej populacji symulując grę w "Małą ewolucję".
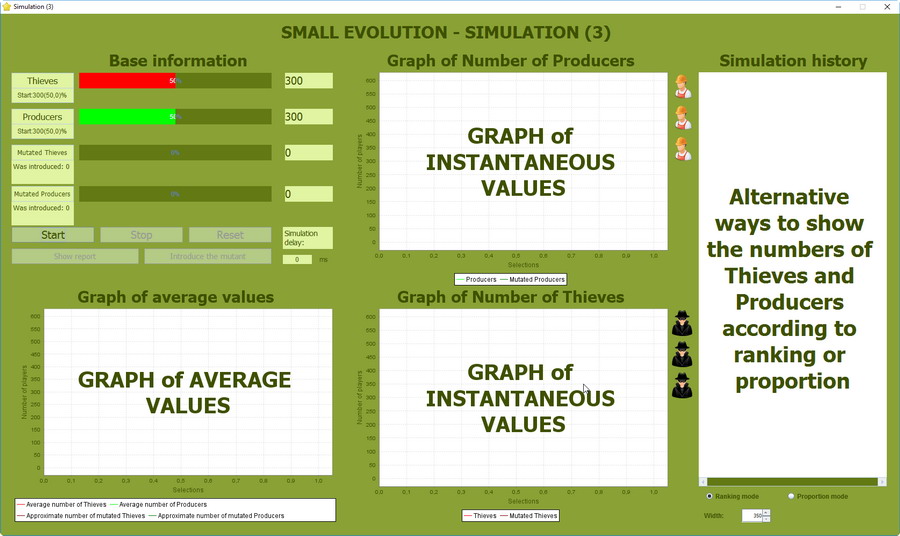
Ekran symulacji gry w "Małą Ewolucję" przed rozpoczęciem symulacji.
Omówmy poszczególne elementy tego ekranu:
-
Informacje podstawowe - w tym obszarze wyświetlane są informacje o stanie początkowym populacji oraz na bieżąco informacje o liczbie Złodziei i Producentów oraz o liczbie mutantów, o ile zostali oni przez nas wprowadzeni do gry.
-
Obszar sterowania symulacją - to grupa przycisków:
- {Start} - którym służy do uruchomienia symulacji;
- {Stop/Restart} - który pozwala na zatrzymanie i wznowienie symulacji. Podczas wznowienia można przyjrzeć się wykresom oraz wprowadzić wcześniej zdefiniowanego mutanta;
- {Reset} - który pozwala na rozpoczęcie symulacji od nowa;
- {Show Report} - po kliknieciu na nim pokaże się ekran podający informacje o przeprowadzonej symulacji;
- {Introduce the mutant} - Za pomocą tego przycisku możemy do badanej populacji wprowadzić uprzednio zdefiniowango mutanta;
- i okienko {Simulation delay} - służące do spowolnienia symulacji, tak by lepiej można było przyglądać się wynikom;
-
Wykres wartości średnich - Wykres ten pokazuje średnie wartości liczby Złodziei i Producentów w badanej populacji w ciągu symulacji. Góra lub wierzchołek wykresu wskazuje miejsce, w którym dobiegł końca cykl.
-
Wykres liczby Producentów - Wykres ten pokazuje rzeczywistą liczbę Producentów w badanej populacji po każdym cyklu.
-
Wykres liczby Złodziei - Wykres ten pokazuje rzeczywistą liczbę Złodziei w badanej populacji po każdym cyklu.
-
Okno przebiegu symulacji - Okno, w którym w sposób graficzny przedstawiana jest historia wszyskich rund i wszystkich cyklów. Informacje te mogą być podane w dwojaki sposób:
- W trybie {Ranking mode} czerwony piksel reprezentuje Złodzieja, a zielony Producenta. Piksele ułożone są od góry do dolu tak jakie miejsca w rankingu zajmują odpowiedni przedstwiciele. I tak jeśli najwięcej punktów zdobył pewien Złodziej i zaraz po nim jest kolejny Złodziej, a po tej dwójce jest sześciu Producentów, wówczas na górze mamy dwa piksele czerwone a poniżej sześć zielonych.
- W trybie {Proportion mode} wyświetlana jest tylko proporcja Złodziei do Producentów, ale Uwaga! nie w całej populacji, lecz tylko tych, którzy potencjalnie przeszliby selekcję pod danej rundzie.
Poniżej tego okna umieszczone jest pole, którym możemy określać szerokość okna przebiegu symulacji.
Opis techniczny programu:
Przebieg symulacji
Poniżej opisany jest algorytm symulacji zaimplementowany w programie
-
Na podstawie danych wprowadzonych przez użytkownika tworzona jest populacja, czyli lista osobników z określeniem jakiego typu są.
- Dopuszczalne typy to: Złodziej, Producent.
-
Z zakresu podanego przez użytkownika w sposób losowy określana jest z pomocą funkcji Random.nextInt jest długość cyklu
-
Realizowana jest runda
-
Licznik rund jest zwiększany o jeden
-
Ustalany jest ranking osobników na podstawie zgromadzonych przez nich punktów. Ranking ten jest wizualizowany w oknie historii w postaci słupka o szerokości jednego piksela. Możliwe są dwie wizualizacje w tym oknie:
- tak, jak ustawione są osobniki w rankingu (każdy piksel w pionie odpowiada jednemu osobnikowi)
- w postaci podania proporcji strategii tych którzy po tej rundzie przeszliby przez selekcję
-
Jeżeli licznik rund osiągnął długość cyklu to:
- Zerowany jest licznik rund
- Realizowana jest selekcja
- Na podstawie wyselekcjonowanych osobników realizowane jest odtworzenie populacji na podstawie algorytmu odtworzenia populacji użytego w programie.
- W ten sposób odtworzonej populacji zerowane są konta wszystkich osobników.
- Program oblicza wartości statystyczne, aktualizuje wykresy
- Program rozpoczyna następny cykl. Program idzie do punktu B
-
Jeżeli licznik rund nie osiągnął długość aktualnego cyklu, cykl jest kontynuowany. Program wraca do punktu C
Liczenie średniej

- Program pamięta ile było poszczególnych strategii (złodziei/producentów/zmutowanych złodziei/zmutowanych producentów) na zakończenie każdego cyklu.
- Wyświetlane w oknie "Graph of average values" wartości to średnie arytmetyczne tych wartości. Przykładowo dla złodziei będzie suma liczby złodziei po każdym cyklu podzielona przez liczbę cykli.
Algorytm odtworzenia populacji
-
Lista wyselekcjonowanych osobników jest ustawiana w losowej kolejności, lista ta określana jest mianem Listy Protoplastów Nowej Populacji (PNP).
-
Analizowane są po kolei osobniki z tej listy.
- Osobnik jest klonowany i tylko klon dodawany do populacji.
- Jeśli liczba osobników w populacji jest równa liczebności populacji to proces populacji jest kończony. Program idzie do punktu C.
- Jeśli liczba osobników w populacji jest mniejsza liczebności populacji to przechodzimy do kolejnego osobnika z listy PNP. W przypadku gdy klonowany osobnik był ostatnim osobnikiem tej listy, program przechodzi do jej początku
- Zwracana jest otrzymana lista populacji.
Wprowadzanie mutanta
- Mechanizm mutowania jest zaimplementowany tak, że Mutant wprowadzany jest po wykonaniu algorytmu odtworzenia populacji. Konsekwencją tego jest fakt, że w momencie rozpoczęcia dalszej symulacji wszyscy osobnicy mają taki sam, umownie zerowy, dorobek punktowy, w tym również nasz nowo zmutowany osobnik.
Pobranie programu 
 Program komputerowy służący do przeprowadzania symulacji gry "Mała ewolucja" jest dostępny Pro Publico Bono na zasadzie Licencji Creative Commons. Oznacza, że użytkownikom przekazuje się następujące prawa:
Program komputerowy służący do przeprowadzania symulacji gry "Mała ewolucja" jest dostępny Pro Publico Bono na zasadzie Licencji Creative Commons. Oznacza, że użytkownikom przekazuje się następujące prawa:
-
Uznanie autorstwa. (BY) Wolno kopiować, rozprowadzać, przedstawiać i wykonywać objęty prawem autorskim utwór oraz opracowane na jego podstawie utwory zależne pod warunkiem, że zostanie przywołane nazwisko autora pierwowzoru.
-
Użycie niekomercyjne. (NC) Wolno kopiować, rozprowadzać, przedstawiać i wykonywać objęty prawem autorskim utwór oraz opracowane na jego podstawie utwory zależne jedynie do celów niekomercyjnych.
-
Na tych samych warunkach. (SA) Wolno rozprowadzać utwory zależne jedynie na licencji identycznej do tej, na jakiej udostępniono utwór oryginalny.

Mała ewolucja - symulacje komputerowe

Niniejszy rozdział pokazuje kilka symulacji i omawia, jak zmiana wybranych parametrów zmienia skład populacj w kolejnych cyklach. Badane będą procesy zachodzące w składzie populacji w zależności od:
zmienności długości cyklu,
zmienności liczebności populacji,
zmienności siły selekcji,
zbadamy również jak zmieni się skład populacji gdy wprowadzimy do niej:
Mutanta Negatywnego,
Mutanta Pół-Pozytywnego i na koniec
Mutanta W-Pełni-Pozytywnego.
Zaobserwowane wnioski podamy na końcu niniejszego rozdziału.
Analizy bez mutacji - zmieniamy Długość Cyklu:

Podczas tej analizy zmienianym parametrem będzie długość cyklu, czyli liczba rund przed selekcją i odtworzeniem populacji. Zobaczmy jak wpływa to na zmiany w składzie populacji.
Analizy bez mutacji - cykl od 1 do 100
W zakresie zmienności długości cyklu od 1 do 100 obserwowana jest względna stałość średniego składu populacji. Badana populacja liczy 600 osobników. Liczba Producentów zmienia się w granicach 100-400, natomiast Złodziei w zakresie 200-500. Widać, że symulacja potwierdza poprawność modelu teoretycznego.
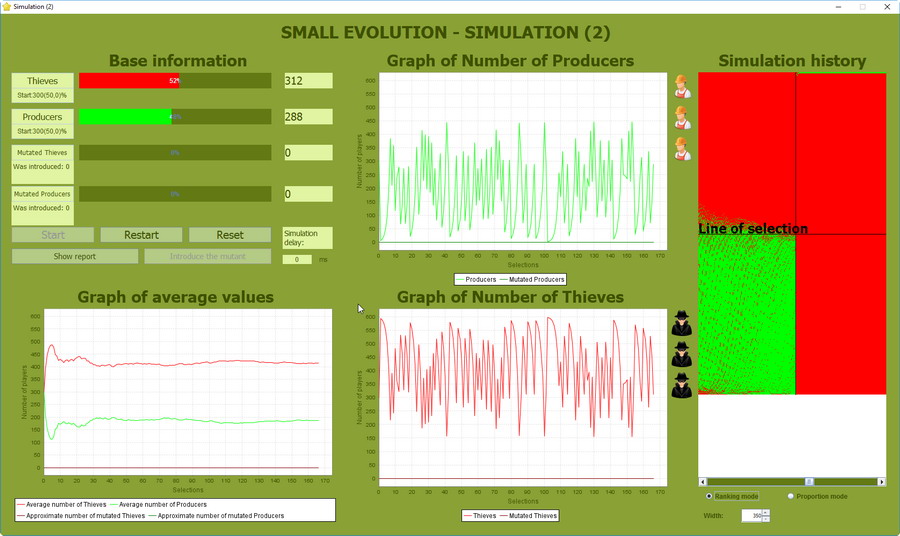
Analizy bez mutacji - cykl od 1 do 400
W zakresie zmienności długości cyklu od 1 do 400 obserwowana jest względna stałość średniego składu populacji. Liczebność Producentów zmienia się w granicach 1-450, natomiast Złodziei w zakresie 150-599. Model teoretyczny jest dalej poprawny ale zastanawiające jest, że obie populacje ocierają się o wartości graniczne, w przypadku Producentów grozi to wyginięciem (zniknięciem z populacji), a w przypadku Złodziei pełną dominacją (populacja będzie składała się wyłącznie ze Złodziei).

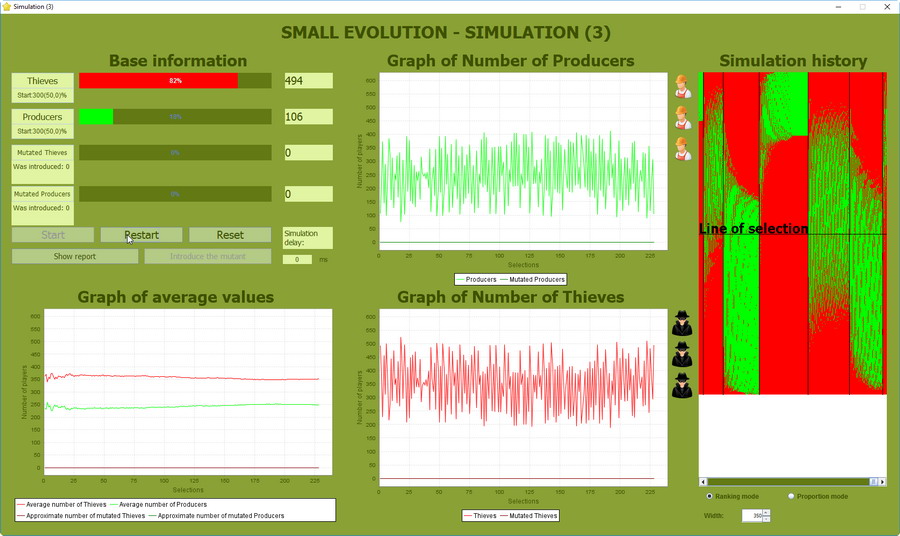
Analizy bez mutacji - cykl od 1 do 600
W zakresie zmienności długości cyklu od 1 do 600 obserwowana jest względna stałość średniego składu populacji. Liczebność Producentów zmienia się w granicach 1-450, natomiast Złodziei w zakresie 150-599. I tu, jak widać, symulacja wywraca model teoretyczny. Model ten bowiem nie uwzględnił amplitudy wahań populacji.
Zanotujmy, że populacja nasyciła się w 100% Złodziejami w okolicy 325 cyklu.

Analizy bez mutacji - cykl od 1 do 800
W zakresie zmienności długości cyklu od 1 do 800 symulacja ponownie wywraca model teoretyczny.
Zanotujmy, że populacja nasyciła się w 100% Złodziejami w okolicy 145 cyklu.
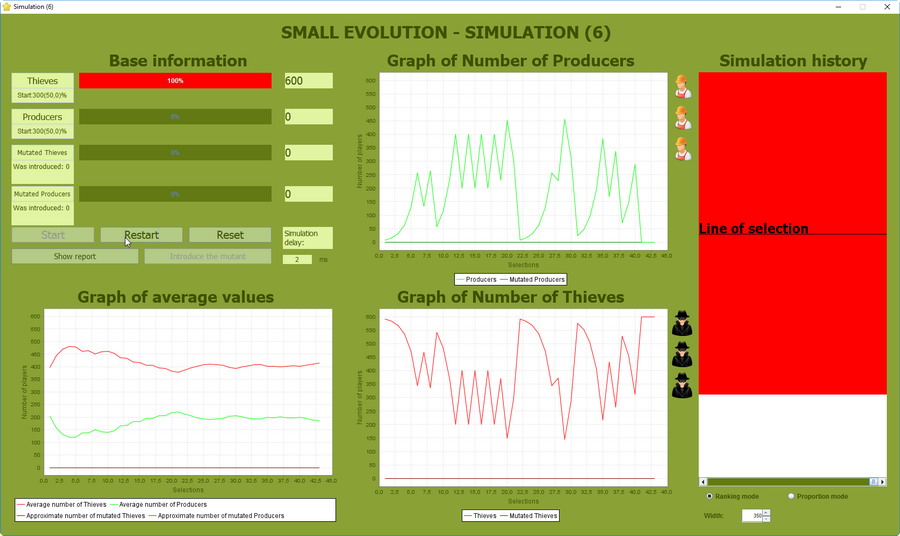
Analizy bez mutacji - cykl od 1 do 1000
W zakresie zmienności długości cyklu od 1 do 1000 symulacja ponownie wywraca model teoretyczny.
Zanotujmy, że populacja nasyciła się w 100% Złodziejami jeszcze szybciej niż poprzednio, bo w okolicy 42 cyklu.
Oczywiście, ponieważ mamy do czynienia ze zdarzeniami probabilistycznymi, do całkowitego opanowania populacji przez Złodziei może dojść w każdym cyklu. Jednak po przeprowadzeniu kulkunastu symulacji dla różnych długości cyklu można odkryć następującą regułę:
prawdopodobieństwo pełnej eliminacji Producentów.
Analizy bez mutacji - zmieniamy Liczebność Populacji:

Podczas tej analizy zmienienym parametrem będzie liczebność populacji, czyli sumaryczna liczba Złodziei i Producentów. Natomiast nie będziemy zmieniać zakresu długość cyklu, będzie on wynosił od 1 do 100. Zobaczmy jak wpływa to na zmiany w składzie populacji.

Liczebność populacji 20
Złodzieje opanowują całą populację po 34 cyklach. Zakres amplitudy zmienności Producentów 2-12, a Złodziei 8-18.
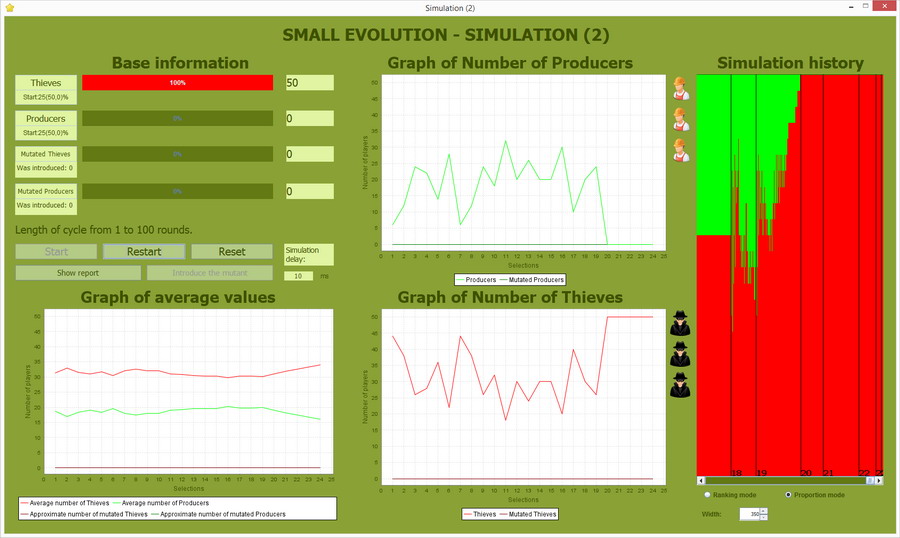
Liczebność populacji 50
Złodzieje opanowują całą populację po 20 cyklach. Zakres amplitudy zmienności Producentów 6-30, a Złodziei 20-44.

Liczebność populacji 100
Nawet po 600 cyklach nie doszło do zdominowania populacji przez Złodziei. Zakres amplitudy zmienności Producentów 5-70, a Złodziei 30-95.
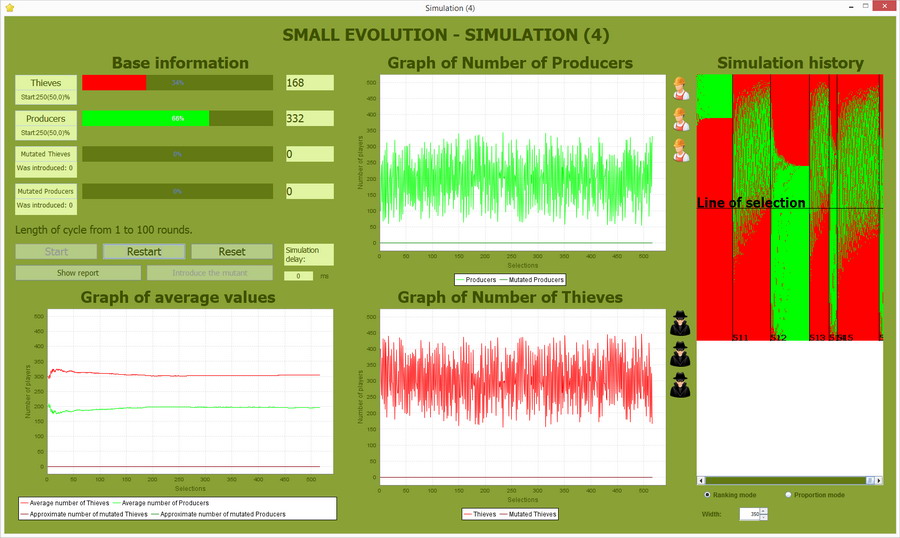
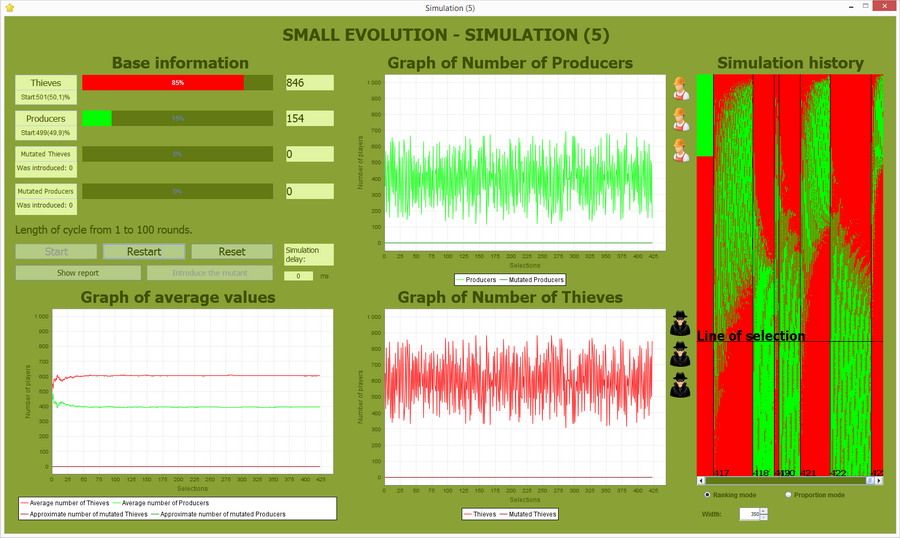
Liczebność populacji 500
Nawet po 600 cyklach nie doszło do zdominowania populacji przez Złodziei. Zakres amplitudy zmienności Producentów 50-350, a Złodziei 150-450.
Liczebność populacji 1000
Nawet po 425 cyklach nie doszło do zdominowania populacji przez Złodziei. Zakres amplitudy zmienności Producentów 110-700, a Złodziei 300-890.
Na podstawie powyższych symulacji można odkryć następującą regułę:
prawdopodobieństwo pełnej eliminacji Producentów.
Analizy bez mutacji - zmieniamy Siłę Selekcji:

Uwzględniając wyniki dwóch poprzednich symulacji do przeprowadzenia trzeciej przyjmiemy, że długość cyklu będzie należała do zakresu 1 - 100, a populacja będzie stosunkowo liczna = 1000. Teraz zobaczmy jak będzie wpływała na populację zmiana siły selekcji.
W tym miejscu warto zwrócić uwagę na algorytm odtworzenia populacji. Jeśli bowiem funkcja selekcyjna jest:
a/. słaba i w wyniku jej działania populacja traci na przykład 20% swoich członków to proces odtworzenia populacji będzie musiał na podstawie przepuszczonych 80% odtworzyć jedynie brakujące 20% - tym samym tylko niektórzy z przepuszczonych zostaną sklonowani.
b/. silna i w wyniku jej działania populacja traci na przykład 85% swoich członków to proces odtworzenia populacji będzie musiał na podstawie przepuszczonych 15% odtworzyć brakujące 85% - tym samym niektórzy z przepuszczonych zostaną sklonowani po wielokroć.
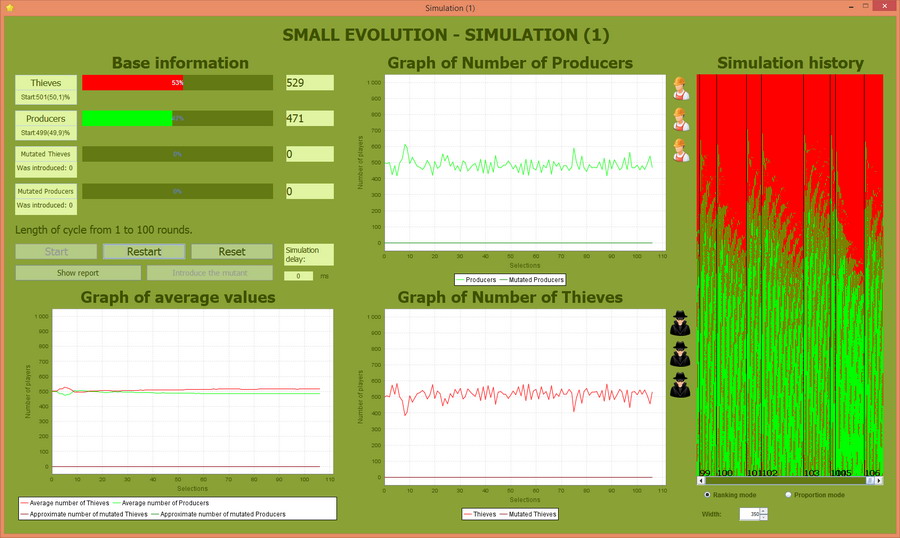
Siła funkcji selekcyjnej 80%
Ponieważ funkcja selekcyjna przepuszcza aż 80% najlepszych osobników, to można ją określić jako "bardzo słabą". Procentowy udział Producentów do Złodziei oscyluje wokół średniej i nie zanosi się na to, żeby Złodzieje zdominowali populację.
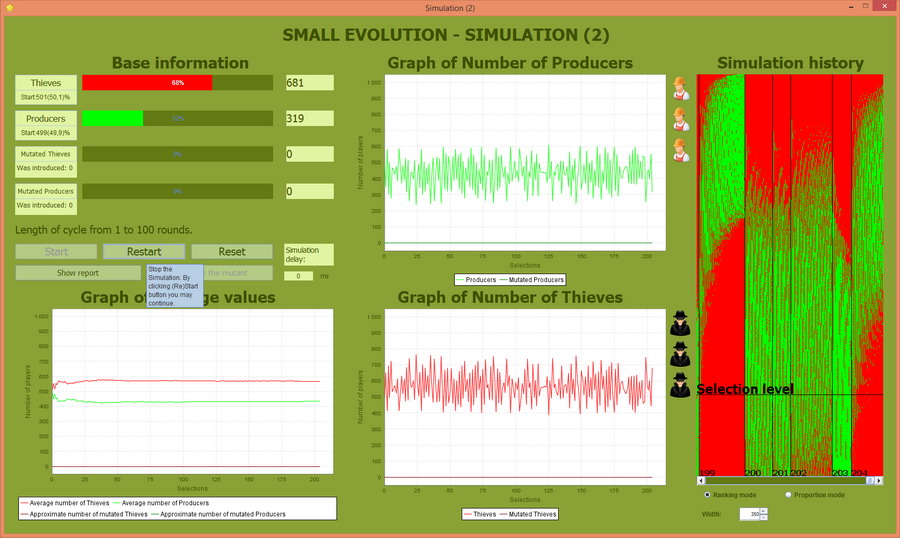
Siła funkcji selekcyjnej 60%
Ponieważ funkcja selekcyjna przepuszcza 60% najlepszych osobników, to można ją określić jako "słabą". Procentowy udział Producentów do Złodziei oscyluje wokół średniej i nie zanosi się na to, żeby Złodzieje zdominowali populację, ale w stosunku do poprzedniej symulacji zauważalny jest wzrost amplitudy.
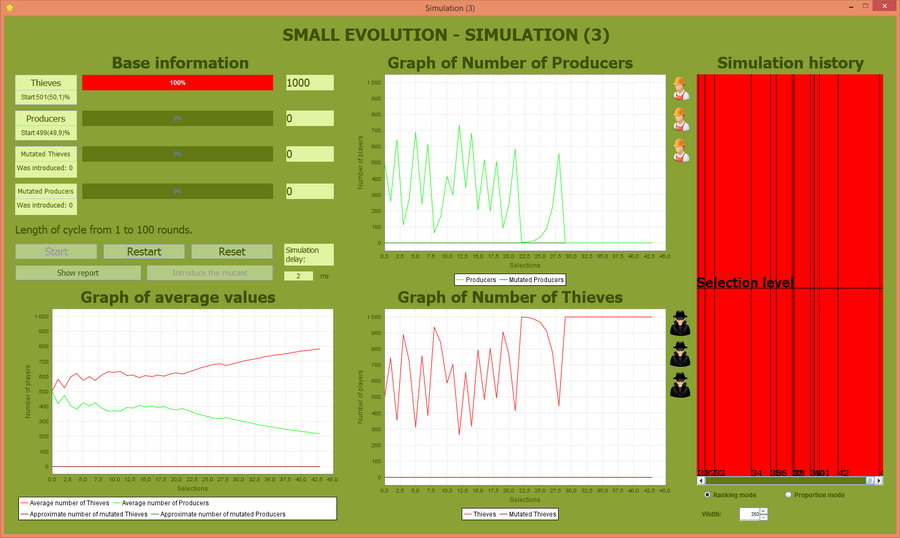
Siła funkcji selekcyjnej 40%
Z poprzednich symulacji pamiętamy, że ustawienie siły selekcji na 50% nie powodowało dominacji Złodziei. Tym razem przy "silnej" funkcji selekcyjnej, która wybiera 40% z najlepszych osobników zauważalny jest punkt zdominowania populacji przez Złodziei już po 28 cyklu.
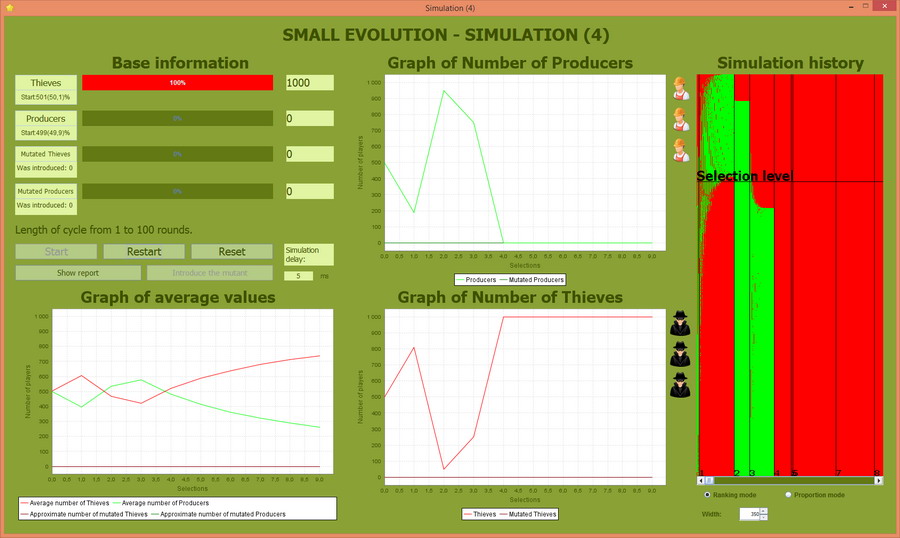
Siła funkcji selekcyjnej 20%
W tej symulacji funkcja selekcyjna jest bardzo silna - do odtworzenia populacji kieruje bowiem zaledwie 20% najlepszych osobników. Jak widać dominacja przez Złodziei następuje prawie natychmiast.
Na podstawie powyższych symulacji można odkryć następującą regułę:
prawdopodobieństwo pełnej eliminacji Producentów.
Analiza z mutacjami - wprowadzamy Mutanta Negatywnego:

Mutant negatywny to taki, który podczas spotkania otrzymuje nieco mniej punktów. Po wprowadzeniu mutanta mamy w populacji trzy typy osobników: Producentów, Złodziei i właśnie jednego świeżo wprowadzonego Mutanta.
Zmutować można zarówno Złodzieja jak i Producenta. Ponieważ do tej pory wygrywali zawsze Złodzieje zmutujemy właśnie jednego z nich. Sama mutacja może być:
-
połowiczna, a więc pogarszać liczbę "urganych" punktów tylko podczas spotkań z innymi Złodziejami, liczba punktów zdobytych podczas spotkań z Producentami nie zmieni się; albo tylko podczas spotkań z Producentami.
-
pełna czyli powoduje "ugrywanie" przez Mutanta nieco mniejszej liczby punktów zarówno w spotkaniach ze Złodziejami jak i Producentami.
Do symulacji zbadane już parametry ustawimy tak, by zapewnić względną trwałość składu populacji, czyli by nie powodowały one szybkiego zdominowania populacji przez Złodziei. Ustawmy je zatem następująco:
Długość cyklu - od 1 do 100 rund
Liczebność populacji - 500 osobników
Siłę funkcji selekcyjnej - 50% [wybieranych jest 50% osobników, którzy zdobyli największą liczbę punktów]
Natomiast mutacja negatywna jest pełna i osłabia Mutanta-Złodzieja w taki sposób, że w spotkaniu z kimkolwiek ugrywa on o jeden punkt mniej od pozostałych.
Okno ustawień początkowych wygląda zatem następująco:

Mutacja negatywna - ekran ustawień początkowych
Podczas symulacji wprowadzono dwukrotnie Negatywnego Mutanta-Złodzieja. Liczba mutantów w populacji przedtawiona jest linią na dole okna "Graph of Number of Thieves".
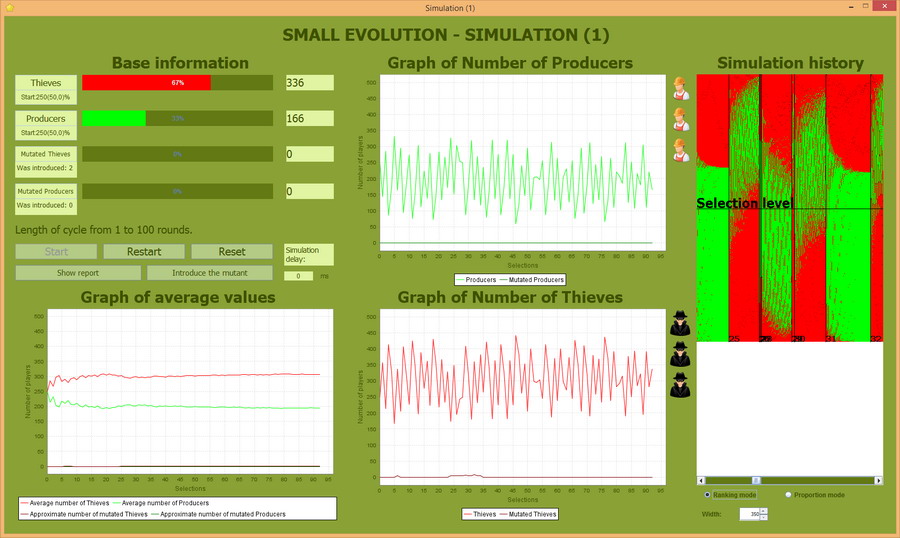
Mutacja negatywna - ekran symulacji
Na powyższym ekranie widać, że negatywnemu Mutantowi udaje się przeżyć w pierwszym przypadku przez jeden cykl, a w drugim przez 9 i nawet udaje mu się zwiększyć swą liczbę w populacji do 4 osobników. Ale w obu przypadkach Mutanci i tak giną.
Program pozwala na przyjżenie się jak plasują się Mutanci w rankingu. Ilustruje to okno "Simulation history", gdzie mutanci reprezentowani są ciemniejszymi pikselami.
Na podstawie powyższych symulacji można odkryć następującą regułę:
składu populacji. Negatywni Mutanci i tak, prędzej czy później, giną.
Analiza z mutacjami - wprowadzamy Mutanta Pół-Pozytywnego:

Tym razem wprowadźmy Pół-Pozytywnego Mutanta Producenta. "Pół" bowiem Mutant ten zdobywa o jeden punkt więcej ale tylko w spotkaniach z innymi Producentami.
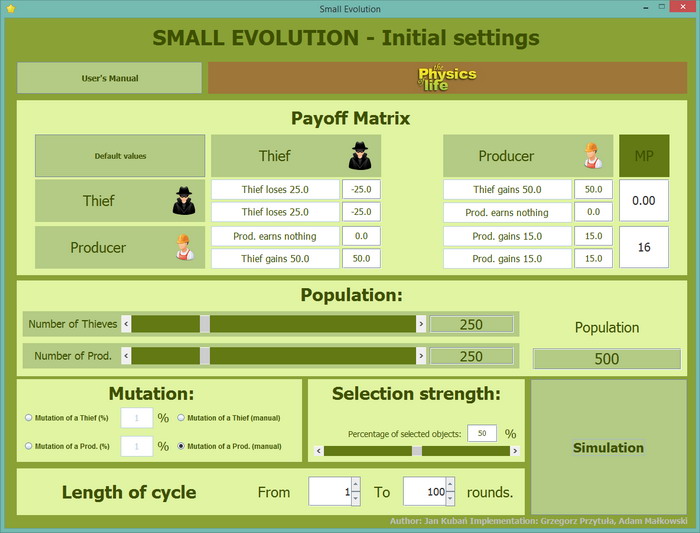
Mutacja pół-pozytywna Producenta - ekran ustawień
Liczbowe wartości, które mówią o ile i gdzie Mutant jest lepszy, przedstawione są po prawej stronie macierzy wypłat - "Payoff Matrix".

Mutacja pół-pozytywna Producenta - ekran symulacji
Widać, że zostały podjęte trzy próby wprowadzenia do populacji Pół-Pozytywnego-Mutanta-Producenta. W pierwszych dwóch przypadkach Mutanci wyginęli, jednak potomstwo trzeciego Mutanta całkowicie zdominowało populację Producentów. Dominacja ta dokonała się w 25 rundach, czyli można powiedzieć, że 500 osobowa populacja została zdominowana przez Mutantów w 25 pokoleniu. Nie jest to zatem wzrost wykładniczy, jeśli bowiem mielibyśmy z nim do czynienia to zdominowanie nastąpiłoby już w 10 pokoleniu.
Na podstawie powyższych symulacji można odkryć następującą regułę:
to jego potomkowie zdominują Populację.
Mechanizm ten nazwany został zapadką ewolucyjną.
Analiza z mutacjami - wprowadzamy Mutanta W Pełni Pozytywnego:

Tę symulację przeprowadzimy wprowadzając W-Pełni-Pozytywnego-Mutanta-Producenta. Mutant ten zdobywa o jeden punkt więcej zarówno w spotkaniach Producentami oraz spotkaniach ze Złodziejami.
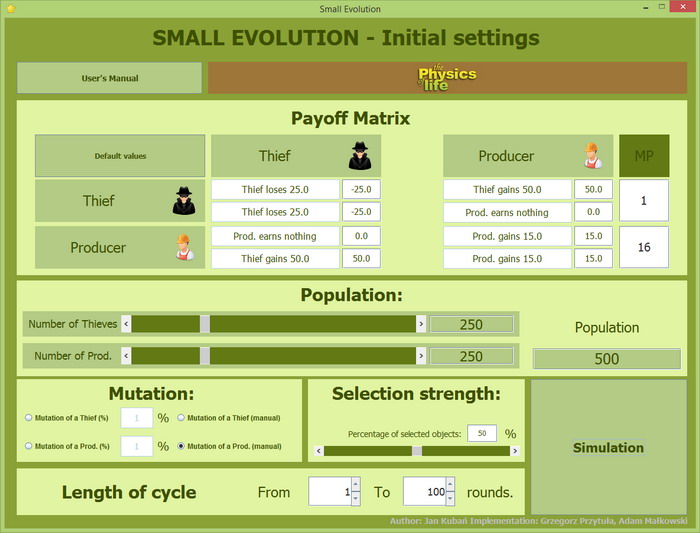
Mutacja w pełni pozytywna - ekran ustawień
Liczbowe wartości, które mówią o ile i gdzie Mutant jest lepszy, przedstawione są po prawej stronie macierzy wypłat - "Payoff Matrix".

Mutacja w pełni pozytywna - ekran symulacji
W tym przypadku Mutanci opanowują cała populację już po 14 pokoleniach, a więc dwukrotnie szybciej niż Pół-Pozytywni-Mutanci z symulacji poprzedniej. Ciekawostką jest to, że nie zawsze W-Pełni-Pozytywnemu-Mutantowi udaje się "zaskoczyć". Wykonując wiele symulacji z tymi ustawieniami okazało się, że czasem takiemu mutantowi nie udaje się przebić przez sito selekcji. Wynika to z tego, że gdy W-Pełni-Pozytywny-Mutant-Producenta wprowadzony jest do populacji, gdy liczy ona stosunkowo mało Złodziei, Złodzieje o wiele częściej spotykają się z Producentami i dlatego bardzo szybko zajmują czołowe lokaty na liście rankingowej. Jeśli natomiast W-Pełni-Pozytywny-Mutant-Producenta cześciej będzie się spotkał się ze Złodziejami niż Producentami to jego stan posiadania bedzie przyrastał wolniej od Producentów, którym uda się uniknąć spotakań ze Złodziejami, i to oni mogą nie dopuścić W-Pełni-Pozytywnego-Mutanta-Producenta do zajęcia na tyle wysokiej pozycji w rankingu, która zapewniłaby mu przejście przez selekcję.
Na podstawie powyższych symulacji można odkryć następującą regułę:
prawie wykładniczo. Czasem taki mutant może nie "zaskoczyć".
Analiza z macierzą "Jak to w życiu"

Podstawowe założenia:
Podobnie jak w klasycznym przykładzie tej gry, zaproponowanym przez John"a Maynard"a Smith"a, rozróżnia się wyłącznie dwa typy strategii (pracusi i złodziei), jednak macierz wypłat dla gry pojedynczego spotkania wygląda "bardziej życiowo":
| „Mała ewolucja” – macierz wypłat „Jak to w życiu” | ||
| Złodziej | Złodziej traci 1 (-1) Złodziej traci 1 (-1) |
Złodziej zyskuje 50 (+50) Producent traci 50 (-50) |
| Producent | Producent traci 50 (-50) Złodziej zyskuje 50 (+50) |
Producent zyskuje 10 (+10) Producent zyskuje 10 (+10) |

Symulacja z tabelą wypłat "Jak to w życiu" - cykl od 1 do 1000
Od razu widać, że przy tej bardzo życiowej tabeli wypłat producenci są wyeliminowani od razu po pierwszym cyklu. Czy w jakiś sposób podważa to nasze dotychczasowe rozważania? Absolutnie nie. Pokazuje to tylko, jak wiele zależy od tego jaką przyjmuje się macierz wypłat oraz prowadzi do kolejnego arcyważnego wniosku.
Otóż jeśli wyginą Producenci, to oczywistym jest, że w kolejnych populacjach pozostaną wyłącznie Złodzieje. W związku z tym wszystkie swoje gry pojedynczego spotkania będą rozgrywali pomiędzy sobą. Czyli żaden ze Złodziei nigdy nie zgromadzi na swoim koncie dodatniej liczby punktów - punktów przetrwania, czyli żaden nie będzie mógł przetrwać. Zatem jeśli Złodzieje wykończą Producentów to w konsekwencji sami też zginą, chyba że... zaczną w inny sposób rozgrywać gry pojedynczego spotkania. Tym arcyważnym wnioskiem jest to, że Złodzieje znajdą się w przymusie współpracy.
Mała ewolucja - Wnioski & Uwagi

Oto podstawowe wnioski, które płyną z przeprowadzonych symulacji:
-
Zwiększenie liczby rund w cyklu zwiększa prawdopodobieństwo eliminacji Producentów.
-
Zwiększenie liczebności populacji zmniejsza prawdopodobieństwo eliminacji Producentów.
-
Zwiększenie liczby eliminowanych przez selekcję osobników zwiększa prawdopodobieństwo eliminacji Producentów.
-
Wprowadzenie Negatywnego Mutanta, w dłuższym wymiarze nie zmienia składu populacji. Negatywni Mutanci i tak, prędzej czy później, giną.
-
Jeśli Pół-Pozytywnemu Mutantowi uda się "zaskoczyć" to jego potomkowie zdominują Populację
-
Potomkowie W-Pełni-Pozytywnego-Mutanta-Producenta dominują populację prawie wykładniczo. Czasem taki mutant może nie "zaskoczyć".
Należy pamiętać, że wnioski te płyną z symulacji określonej:
- takimi, a nie innymi parametrami,
- przy przyjętych takich, a nie innych założeniach,
- i przy przyjęciu takich, a nie innych algorytmów.
Innym bardzo ważnym wnioskiem jest to, że myślenie redukcjonistyczne jest absolutnie niewystarczające do zrozumienia zjawisk populacyjnych. Żeby je należycie zrozumieć trzeba rozszerzyć swój aparat pojęciowy o, co najmniej, myślenie mnogościowe i myślenie teoriogrowe.
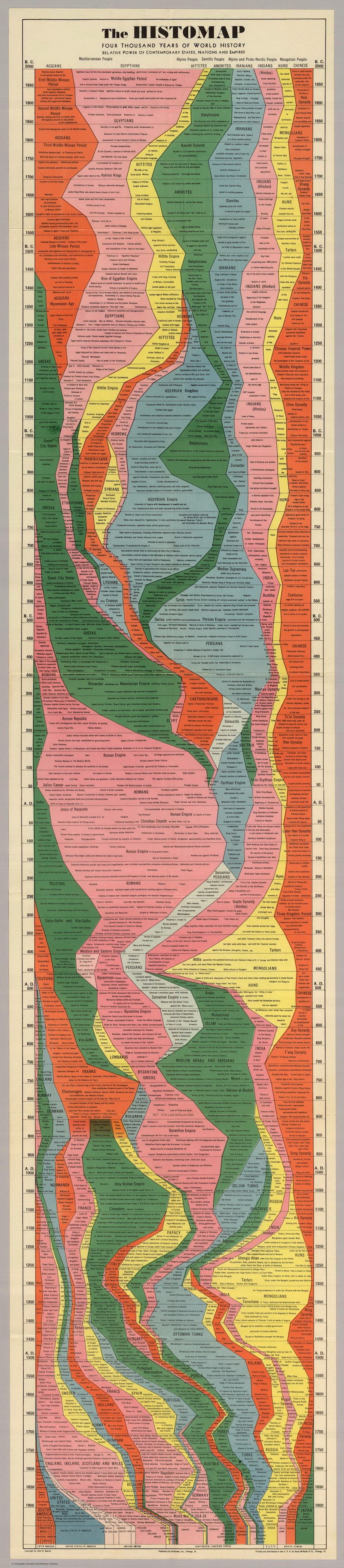
Historia Ludzkich Populacji

Na stronie The Entire History of the World — Distilled Into a Single Gorgeous Chart przedstawiono ciekawą grafikę prezentującą historię procentowego składu dominujących na Świecie populacji ludzkich. W swym charakterze jest ona analogiczna do grafik z symulacji komputerowej.
Ciekawe Linki

-
Human and nature dynamics (HANDY): Modeling inequality and use of resources in the collapse or sustainability of societies
Inwazja obcych? Tajemniczy wirus, który zamieni ludzi w zombi? Wiemy już, jak dojdzie do upadku cywilizacji - ostrzegają amerykańscy naukowcy. - Być może nawet szybciej, niż myślicie. Wizje upadku cywilizacji są tak stare jak ona sama - zaczynając od potopu i Apokalipsy św. Jana, na inwazji zombi i zalaniu świata przez oceany kończąc. Do tej czcigodnej tradycji dołączyło troje naukowców - Safa Motesharrei, matematyk, i Eugenia Kalnay, klimatolożka, oboje z Uniwersytetu w Maryland, oraz Jorge Rivas, politolog z Uniwersytetu Minnesota. Ich wspólny artykuł opublikowało w majowym numerze naukowe pismo "Ecological Economics". Amerykańscy naukowcy zastrzegają, że ich propozycja jest tylko "eksperymentem myślowym". Ewidentnie traktują swój matematyczny model serio. Pokazuje on wspólną dynamikę czterech zmiennych: zasobów natury, zakumulowanego bogactwa ludzkości oraz poziomu konsumpcji dwóch kategorii ludzi - "pospólstwa" i "elit"…

